Was ist eine Bézier-Kurve?

Eine Bézier-Kurve ist eine parametrische Kurve, die in der Computergrafik und im Design verwendet wird, um glatte Kurven und Oberflächen zu erzeugen. Diese Kurven werden mathematisch durch Polynome beschrieben und wurden in der Computergrafikbranche aufgrund ihrer Implementierung in Design- und Modellierungsprogrammen weithin populär.

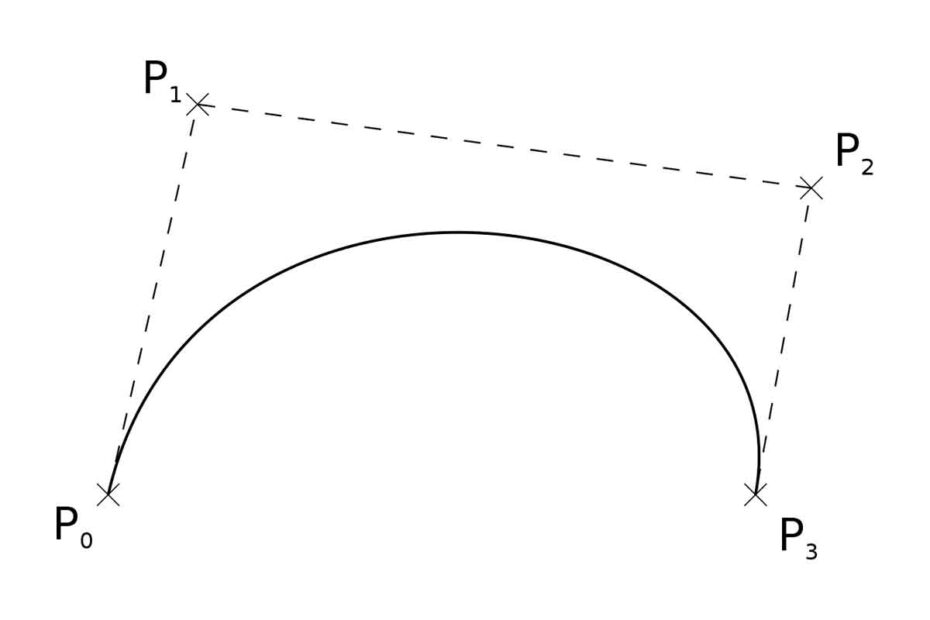
Die Grundform der Bézier-Kurve verwendet vier Punkte:

• Startpunkt (P0): An diesem Punkt beginnt die Kurve.
• Kontrollpunkt 1 (P1): Er bestimmt die Richtung und den Betrag der Krümmung am Anfang.
• Kontrollpunkt 2 (P2): Bestimmt die Richtung und Größe der Krümmung am Ende.
• Endpunkt (P3): ist der Punkt, an dem die Kurve endet.

Die Position eines Punktes auf der Bézier-Kurve wird durch eine Linearkombination dieser Punkte berechnet und in der Regel durch die Bernsteinsche kubische Polynomformel definiert. Die genaue Form der Kurve wird durch die Lage der Kontrollpunkte bestimmt.

Merkmale und Vorteile von Bézier-Kurven

Die besonderen Eigenschaften von Bézier-Kurven bieten eine Reihe von Vorteilen, die dazu geführt haben, dass sie in vielen Branchen, darunter auch im Grafikdesign, eingesetzt werden:

• Präzise Steuerung: Durch die Manipulation der Kontrollpunkte können die Nutzer die Form der Bézier-Kurve leicht an ihre Bedürfnisse anpassen.
• Glattheit: Sie gewährleisten Glätte und Kontinuität und sind daher ideal für die Darstellung von Konturen und glatten Formen.
• Modularität: Sie können verkettet oder miteinander verbunden werden, um längere oder komplexere Pfade zu bilden, wobei die Kontinuität zwischen den Segmenten erhalten bleibt.
• Flexibilität: Bézier-Kurven gibt es in verschiedenen Abstufungen, von linearen bis hin zu höheren Abstufungen, die je nach Bedarf unterschiedliche Komplexitäts- und Flexibilitätsgrade bieten.
• Effiziente Interpolation: Trotz ihrer Flexibilität können Bézier-Kurven mit Algorithmen wie De Casteljau effizient ausgewertet werden.
• Kompakte Darstellung: Eine Bézier-Kurve ist vollständig durch ihre Kontrollpunkte definiert. Das bedeutet, dass unabhängig von ihrer Länge oder Komplexität nur eine feste Anzahl von Punkten erforderlich ist, um sie darzustellen.
• Affine Invarianz: Bézier-Kurven behalten ihre relative Form bei affinen Transformationen wie Verschiebungen, Drehungen und Skalierungen bei.
• Sichtbarkeit der Hüllkurve: Die Kontrollpunkte bilden eine konvexe Umhüllung um die Kurve. Das ist nützlich, weil es garantiert, dass die Kurve diesen durch die Kontrollpunkte begrenzten Raum nicht verlässt.
• Intuitivität: Für Designer/innen und Künstler/innen bieten Bézier-Kurven eine intuitive Arbeitsweise, da die Bewegung oder Anpassung eines Kontrollpunktes sofort zeigt, wie sie sich auf die Form der Kurve auswirkt.
• Weit verbreitete Anwendung: Aufgrund ihrer Nützlichkeit und Vielseitigkeit werden Bézier-Kurven von praktisch allen Grafikdesign-, 3D-Modellierungs- und verwandten Grafik- und Animationssoftware unterstützt.

Arten von Bézier-Kurven

Es gibt verschiedene Arten von Bézier-Kurven, die nach der Anzahl der verwendeten Kontrollpunkte unterschieden werden. Die Komplexität und Flexibilität der Kurve nimmt mit der Anzahl der Kontrollpunkte zu. Im Folgenden beschreiben wir die Eigenschaften der gängigsten Typen:

Lineare Bézier-Kurven (ersten Grades)

• Sie verwenden 2 Kontrollpunkte: einen Anfangspunkt und einen Endpunkt.
• Zwischen diesen beiden Punkten entsteht eine gerade Linie.
• Die Gleichung einer linearen Bézier-Kurve ist einfach eine lineare Interpolation zwischen zwei Punkten.

Quadratische Bézier-Kurven (zweiten Grades)

• Sie verwenden 3 Kontrollpunkte: einen Anfangspunkt, einen Kontrollpunkt und einen Endpunkt.
• Sie sind nützlich, um Abschnitte von Parabeln darzustellen.
• Sie werden hauptsächlich von der Position des zentralen Kontrollpunkts beeinflusst.

Kubische Bézier-Kurven (dritten Grades)

• Sie verwenden 4 Kontrollpunkte: einen Startpunkt, zwei Kontrollpunkte und einen Endpunkt.
• Dieser Typ wird am häufigsten in Grafikdesign und Animation verwendet, da er eine gute Kombination aus Kontrolle und Glätte bietet.
• Die beiden Kontrollpunkte bestimmen die Tangente und die Form der Kurve am Anfang und am Ende.

Bézier-Kurven höheren Grades

• Es ist möglich, Bézier-Kurven mit mehr als 4 Kontrollpunkten zu definieren, indem du ihren Grad erhöhst.
• Je höher der Grad, desto komplexer und flexibler ist die Kurve.

In der Praxis können Bézier-Kurven mit sehr hohem Grad jedoch schwer zu kontrollieren sein und unerwünschte Schwingungen aufweisen. Aus diesem Grund ist es üblich, statt einer Kurve mit sehr hohem Grad mehrere Bézier-Kurven mit niedrigerem Grad aneinander zu ketten, um komplexe Trajektorien zu bilden.

Obwohl es viele Arten von Bézier-Kurven gibt, werden in vielen Anwendungen, vor allem im Grafikdesign, am häufigsten kubische Kurven verwendet, weil sie ein ausgewogenes Verhältnis zwischen Kontrolle und Komplexität bieten.

Wofür werden Bézier-Kurven verwendet?

Dank ihrer Vielseitigkeit und dem Maß an Kontrolle, das sie bieten, werden Bézier-Kurven in einer Vielzahl von Bereichen eingesetzt, die wir im Folgenden beschreiben:

• Grafikdesign und Typografie: In Vektordesignprogrammen wie Adobe Illustrator oder CorelDRAW werden Bézier-Kurven verwendet, um Formen zu erstellen und zu verändern. Sie sind auch grundlegend für die Definition von Zeichenkonturen in digitalen Schriftarten.
• Animation und 3D-Modellierung: In Blender, Maya oder 3ds Max können Bézier-Kurven verwendet werden, um Bewegungspfade zu zeichnen, Oberflächen zu erstellen und Formen zu definieren.
• Industriedesign und CAD: Im computergestützten Design können diese Kurven verwendet werden, um komplexe Formen und Oberflächen genau darzustellen.
• Automobil- und Luftfahrtdesign: Bézier-Kurven sind für die Gestaltung von glatten und aerodynamischen Oberflächen unerlässlich.
• Benutzeroberfläche: In einigen grafischen Oberflächen können Übergänge und Animationen auf Bézier-Kurven basieren, um natürlichere und flüssigere Bewegungen zu erreichen.
• Videospiele: Sie werden für Animationen, Objektbahnen und Oberflächenmodellierung verwendet.
• Simulationen: Zum Nachzeichnen von Flugbahnen oder Bewegungen in Physiksimulationen oder jeder anderen Art von Simulation, die einen fließenden Übergang zwischen Punkten erfordert.
• Videobearbeitung und visuelle Effekte: Für die Erstellung flüssiger Kamerabewegungen, Animationen und Übergangseffekte.
• Medizin: In der medizinischen Visualisierung und bei der Erstellung von individuellen Implantaten und Prothesen.
• Musik: Für die Interpolation von Werten in Musikbearbeitungs- und -erstellungsprogrammen, z. B. zur Modulation von Effekten oder für Übergänge zwischen Noten.